

Union-Find Data Structure
Get started
জয় শ্রী রাম
🕉-
Union-Find is NOT applicable on DIRECTED Graphs. It is only applicable to Undirected Graphs.
- Most problems that can be solved by Union-Find, can also be solved by DFS Connected Components approach.
The efficiency of an algorithm sometimes depends on using an efficient data structure. A good choice of data structure can reduce the execution time of an algorithm and Union-Find is a data structure that falls in that category.
A Union-Find data structure can be used to maintain knowledge of the connected components of a graph, and query for them quickly.
Union-find represents a subset using a rooted tree where each node points to its parent instead of its children. Finding out which subset we are in is simple, for we keep traversing up the parent pointers until we hit the root. Unioning two subsets is also easy. Just assign the root of one of two trees to point the root of another tree. So now all elements of the two trees have the same root and hence are now a same subset.
Implementation details have a big impact on asymptotic performance. Always selecting the larger (or taller) tree as the root in a merger guarantees logarithmic height trees. Retraversing the path traced on each find and explicitly pointing all nodes on the path to the root (called path compression) reduces the tree to almost constant height. Union Find is a fast, simple data structure that every programmer should know about. It does not support breaking up subsets created by unions, but usually that is not an issue.
Now let's dive into it in details. Let’s say, you have a set of N elements which are partitioned into further subsets, and you have to keep track of connectivity of each element in a particular subset or connectivity of subsets with each other. To do this operation efficiently, you can use Union-Find Data Structure.
Let’s say there are 5 people A, B, C, D, E. A is a friend of B, B is a friend of C and D is a friend of E. As we can see:
1) A, B and C are connected to each other.
2) D and E are connected to each other.
So we can use Union Find Data Structure to check whether one friend is connected to another in a direct or indirect way or not. We can also determine the two different disconnected subsets. Here 2 different subsets are {A, B, C} and {D, E}.
We have three important operations here :
Find(A) – Finds the component that A belongs to and returns the root of that component.
Union(A, B) – Connects two elements A and B by making the root of A point to the root of B. This is done by doing: parent(root(A)) = root(b).
Find(A, B) – Finds if A and B belong to the same component, i.e, if A and B have same root, i.e, if Find(A) == Find(B).
Example: You have a set of elements S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Here you have 10 elements (N = 10 ).We can use an array Arr to manage the connectivity of elements. Arr[ ] indexed by elements of set, having size of N (as N elements in set) and can be used to manage the above operations.
Assumption: A and B objects are connected only if Arr[ A ] = Arr [ B ].
Now how we will implement above operations :
Find (A, B): check if Arr[ A ] is equal to Arr[ B ] or not. Union (A, B) – Connect A to B and merge the components having A and B by changing all the elements ,whose value is equal to Arr[ A ], to Arr[ B ].
Initially there are 10 subsets and each subset has single element in it.

When each subset contains only single element, the array Arr is:

Let’s perform some Operations: 1) Union(2, 1)

Arr will be:

2) Union(4, 3)
3) Union(8, 4)
4) Union(9, 3)
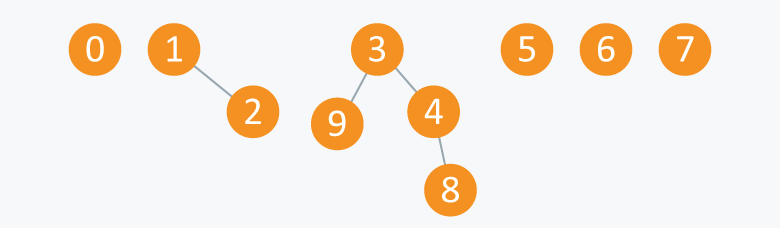
Arr will be:

5) Union(6, 5)

Arr will be:

After performing some operations of Union(A ,B), you can see that now there are 5 subsets. First has elements {3, 4, 8, 9}, second has {1, 2}, third has {5, 6}, fourth has {0} and fifth has {7}. All these subsets are said to be Connected Components.
One can also relate these elements with nodes of a graph. The elements in one subset can be considered as the nodes of the graph which are connected to each other directly or indirectly, therefore each subset can be considered as connected component.
From this, we can infer that Union-Find data structure is useful in Graphs for performing various operations like connecting nodes, finding connected components etc.
Let’s perform some Find(A, B) operations. 1) Find (0, 7) – as 0 and 7 are disconnected ,this will gives false result.
2) Find (8, 9) - though 8 and 9 are not connected directly ,but there exist a path connecting 8 and 9, so it will give us true result.
When we see above operations in terms of components, then :
Union(A, B) – Replace components containing two objects A and B with their union.
Find(A, B) – check if two objects A and B are in same component or not.
So if we perform operation Union(5, 2) on above components, then it will be :
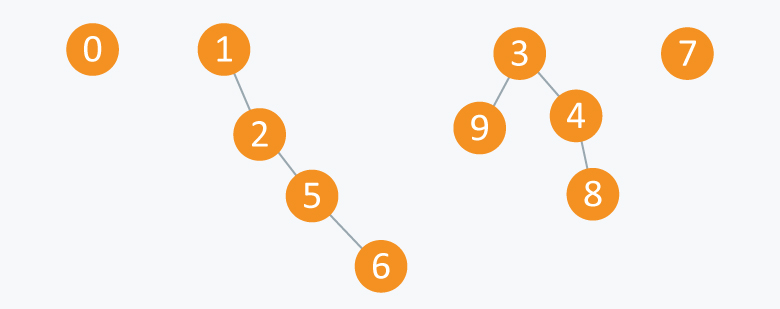
Now the Arr will be:

Implementation:
Initially there are N subsets containing single element in each subset, so to initialize array we will use initialize ( ) function.
void initialize( int Arr[ ], int N)
{
for(int i = 0;i < N;i++) Arr[ i ]=i ; //initially every element is its own root
}
//returns true,if A and B are connected, else it will return false.
boolean find( int Arr[ ], int A, int B)
{
return (Arr[A] == Arr[B]);
}
//change all entries from Arr[ A ] to Arr[ B ].
void union(int Arr[ ], int N, int A, int B)
{
int TEMP=Arr[ A ];
for(int i=0; i < N;i++)
{
if(Arr[ i ] == TEMP)
Arr[ i ] = Arr[ B ];
}
}
As loop in Union function iterates through all the N elements for connecting two elements. So performing this operation on N objects will take O(N2) time, which is quite inefficient.
Now the fun part begins:
Let’s try another approach:
Idea: parent[ A ] is a parent of A.
We can consider a root element of each subset, which is only one special element in that subset having itself as the parent. Let’s say R is a root element, then parent[ R ] = R.
To make it more clear,let’s take a subset S = {0, 1, 2, 3, 4, 5}
Initially each element is the root of itself in all subsets, as parent[ i ] = i, where i is element in the set, therefore root(i) = i.

Performing Union(1, 0) will connect 1 to 0 and will set root(0) as the parent of root(1). As root(1) = 1, and root(0) = 0, therefore value of parent[ 1 ] will be changed from 1 to 0. It will make 0 as a root of subset containing elements {0, 1}.
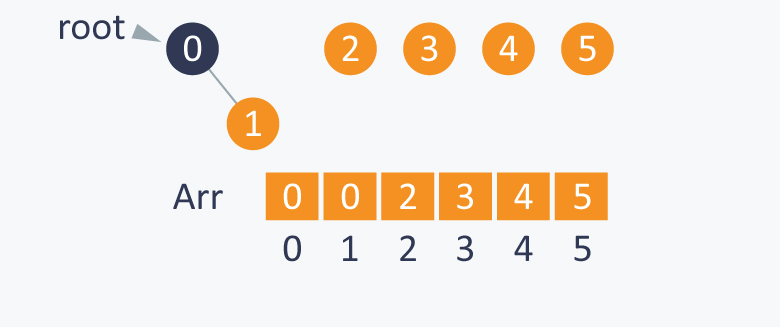
Now performing Union(0, 2), will indirectly connect 0 to 2, by setting root(2) as the parent of root(0). As root(0) is 0 and root(2) is 2, therefore it will change value parent[ 0 ] from 0 to 2. Now 2 will be the root of subset containing elements {2, 0, 1}.

Similarly Union(3, 4) will indirectly connect 3 to 4, by setting root(4) as the parent of root(3). As root(3) is 3 and root(4) is 4, therefore it will change value of parent[ 3 ] from 3 to 4. It will make 4 as a root of subset containing elements {3, 4}.

Performing Union(1, 4 ) will indirectly connect 1 to 4, by setting root(4) as the parent of root(1). As root(4) is 4 and root(1) is 2, therefore it will change value of parent[ 2 ] from 2 to 4. It makes 4 as root of set containing elements {0, 1, 2, 3, 4}.
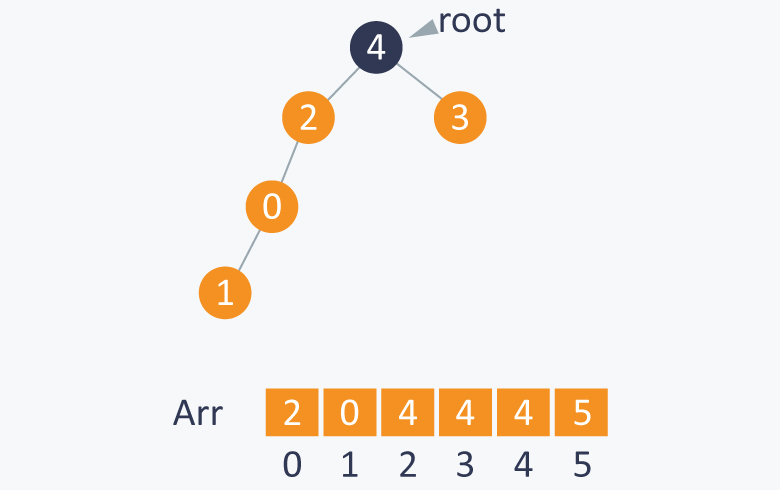
After each step you can observe the change in array Parent also.
After performing required Union(A, B) operations, we can easily perform the Find(A, B) operation to check whether A and B are connected or not. It can be checked by calculating roots of both A and B. If roots of A and B are same, that means both A and B are in same subset and are connected.
Now how to calculate root of a element ?
As we know that parent[ i ] is the parent of i (where i is the element of set),then the root of i is parent[ parent[ parent[ ……parent[ i ]…… ] ] ] until parent[ i ] is equal to i.
Simply we can run a loop until we get a element which is a parent of itself.
Note: This can be only done when there is no cycle in the elements of subset, otherwise loop will run infinitely.
Find(1, 4) – 1 and 4 have same root as 4, therefore it means they are connected and this operation will give true as a result.
Find(3, 5) – 3 and 5 do not have same root, as root(3) is 4 and root(5) is 5. It means they are not connected and it will give false as a result.
Implementation:
As initially all the elements are parent of itself,which can be done using initialize function discussed above.
//finding root of an element.
int find(int i)
{
while(parent[ i ] != i) //chase parent of current element until it reaches root.
{
i = parent[ i ];
}
return i;
}
/*modified union function where we connect the elements
by changing the root of one of the element */
int union(int A, int B)
{
int root_A = find(A);
int root_B = find(B);
parent[ root_A ] = root_B ; //setting parent of root(A) as root(B).
}
bool find(int A,int B)
{
return (find(A) == find(B)) //if A and B have same root, they are connected.
}
Now as you can see, in worst case, this idea will also take linear time in connecting 2 elements and even in finding that if two elements are connected or not, it will take linear time. Another disadvantage is that while connecting two elements, we do not check which subset has more element than other and sometimes it creates a big problem as in worst case we have to perform approximately linear time operations.
Weighted Union:
We can avoid the above mentioned problem by keeping the track of size of each subset and then while connecting two elements, we can connect the root of subset having smaller number of elements to the root of subset having larger number of elements.
Example:
Here if we want to connect 1 and 5, then we will connect the root of Subset A (subset which contains 1) will be connected to root of Subset B (contains 5), this is because Subset A contains less number of elements than of Subset B.
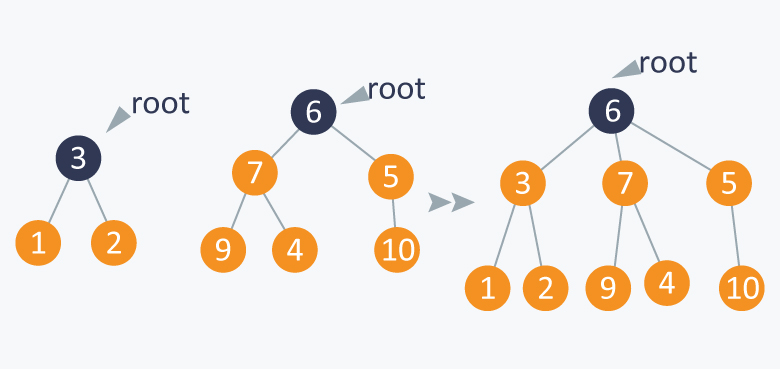
It will balance the tree formed by the above operations. We call this operation as Weighted Union operation .
Implementation:
Initially the size of each subset will be one as each subset will have only one element and we can initialize it in the initialize function discussed above:
size[ ] array will keep track of size of each subset.
//modified initialize function:
void initialize(int parent[ ], int N)
{
for(int i = 0;i < N;i++)
{
parent[ i ] = i ;
size[ i ] = 1;
}
}
root() and find() function will be same as above .
Union function will be modified as we will connect two subsets according to the number of elements in subset.
//modified union function
void weighted-union(int parent[ ],int size[ ],int A,int B)
{
int root_A = find(A);
int root_B = find(B);
if(size[root_A] < size[root_B ])
{
parent[ root_A ] = root_B;
size[root_B] += size[root_A];
}
else
{
parent[ root_B ] = root_A;
size[root_A] += size[root_B];
}
}
Example:
You have a set S = {0, 1, 2, 3, 4, 5} Initially all the subsets have a single element and each element is a root of itself. Initially size[ ] array will be :
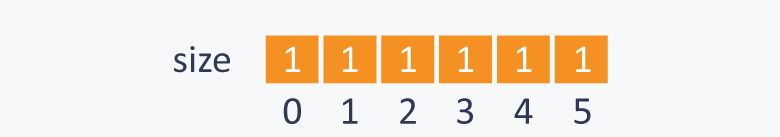
Perform Union(0, 1). Here we can connect any root of any element with root of other one as both the element’s subsets have same size and then we will update the respective size.
If we connect 1 to 0 and make 0 as a root and then size of 0 will change from 1 to 2.

While performing Union(1, 2), we will connect root(2) with root(1) as subset of 2 has less number of elements than number of elements in subset of 1.

Similarly in Union(3, 2), it will connect root(3) to root(2) as subset of 3 has less number of element than number of elements in subset of 2.
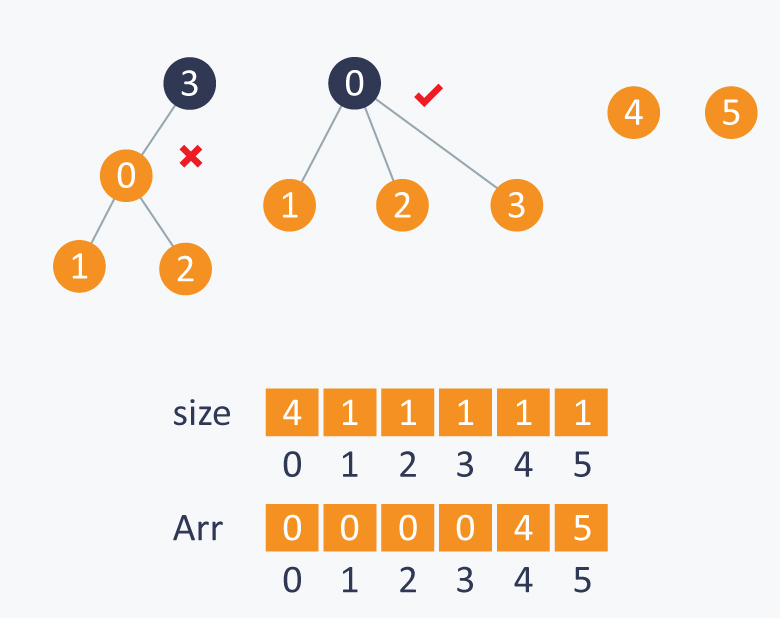
Maintaining a Balanced Tree, will reduce complexity of union and find function from O(N) to O(log2N).
Can we improve further ?
Yes.
Idea: Union with path compression : While computing the root of A, set each i to point to its grandparent (thereby halving the path length), where i is the node which comes in between path, while computing root of A.
// modified root function.
int find(int i)
{
while(parent[ i ] != i)
{
parent[ i ] = parent[ parent[ i ] ] ;
i = parent[ i ];
}
return i;
}
When we use Weighted-union with path compression it takes
O(log*N) for each union find operation,where N is the number of elements in the set.
log *N, usually read "log star", is the iterative logarithm
which is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1.
log*N is much better than log N, as its value reaches at most up to 5 in the real world.
A bit more clarification: log*n is log(log(……log(n))) (recursive log that many times until the number becomes 1). It’s an extremely slowly growing function,
if n = 2^65536 ,
log*(n) = 5.
Notice in the path compression step you link the node to its grandparent ,ultimately decreasing the levels of the tree by bringing nodes closer to the root (tree gets flattened ).
Another implementation of Path Compression is as below where we make the parent of a node to point direct to the root instead of the grandparent:
public int find(int x) {
if (parent[x] != x) parent[x] = find(parent[x]);
return parent[x];
}
See how it compresses the path for all the nodes in between the node on which find was initially called (here, node with value x) and the root in one pass.
Pictorial Representation:
Before Path Compression:
After Path Compression:

Union(F, G):
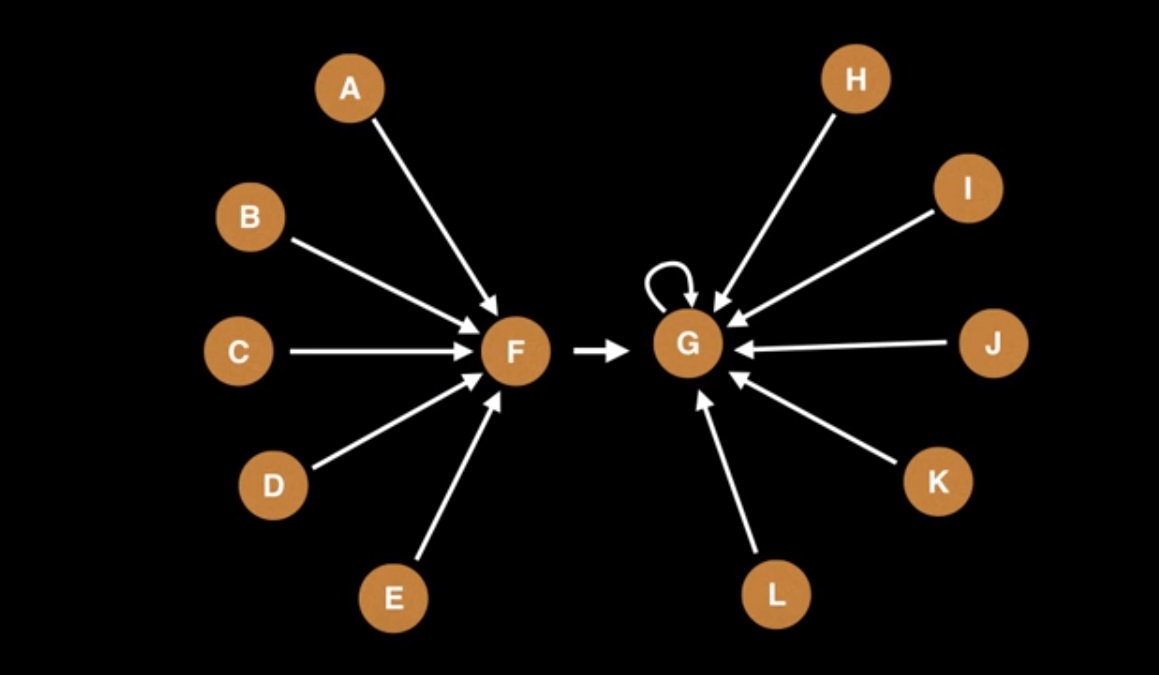
Point to be noted: Path Compression is Lazy Approach and it compresses the path between a
node and it’s root only when the node is processed (i.e, union-ed).
Time Complexity of union() and find() operations:
From discussion above we could conclude that:
-
For Weighted Union Find (also know as, union find by rank) without path compression, time complexity
for both union() and find() =
O(logN). -
For Weighted Union Find (also known as, union find by rank) with path compression, time complexity for both union()
and find() =
O(α(N)) ≈ O(1), where α is the inverse of the Ackerman function.
Applications:
1) As explained above, Union-Find is used to determine the connected components in a graph. We can determine whether 2 nodes are in the same connected component or not in the graph. We can also determine that by adding an edge between 2 nodes whether it leads to cycle in the graph or not. We learned that we can reduce its complexity to a very optimum level, so in case of very large and dense graph we can use this data structure. 2) It is used to determine the cycles in the graph. In the Kruskal’s Algorithm, Union Find Data Structure is used as a subroutine to find the cycles in the graph, which helps in finding the minimum spanning tree. This is explained in great details in 4 Ways to Finding Cycles. and Redundant Connection .Concrete Implementation:
While solving problems using Union-Find concept, for most cases you would be able to reuse the below Union-Find implementation as-is.At The Algorists, my goal is not just to help you get better at problem solving, but also to set you up for success for long-term software engineering career. Notice how we always try to code in a way that can be reused and/or extended. As you progress in your career, your ability to write reusable components would help you maximize your impact, and would play in favour of you get getting promoted. The below example is a very simple example of reusing code, but it could be applied at any scale. Writing reusable code and building reusable components should become your second nature because this is what makes software design and architecture robust and maintainable. Please look at all the Union-Find Problems to see how we reuse the below code.
Java Code:
Login to Access Content
Python Code:
Login to Access Content
I have shown in below chapters how the above code could be used as-is to solve real world problems:
- Longest Consecutive Sequence
- Valid Tree
- Number of Islands
- Number of Provinces
- Redundant Connection
- Accounts Merge
